- !
- Trees: basic concepts
- Binary Trees
- ")Binary Search Tree (BST)
- Binary Tree Transversal
- Balanced vs. Non-balanced Trees
- Big O Notation
- Common Patterns
- Recursion
- Searching Algorithms
- Sorting Algorithms
- Quadric
- Fancy
- Data Structure
- Singly Linked list
- Doubly Linked List
- Stacks
- Queue
- Tree
- Binary heaps
- Priority Queue
- Hash Tables
- Graphs
- adjacency list
- adjacency list vs adjacency matrix
- Graph Traversal
- Dijkstra's Shortest path firt Algorithms
- Dynamic Programming (light introduction)
- Interesting Stuff
- String
- Array
- Math
Its always good to have a look at worst-case time complexities of common data structure operations frequently.
Its always good to have a look at worst-case time complexities of common data structure operations frequently.

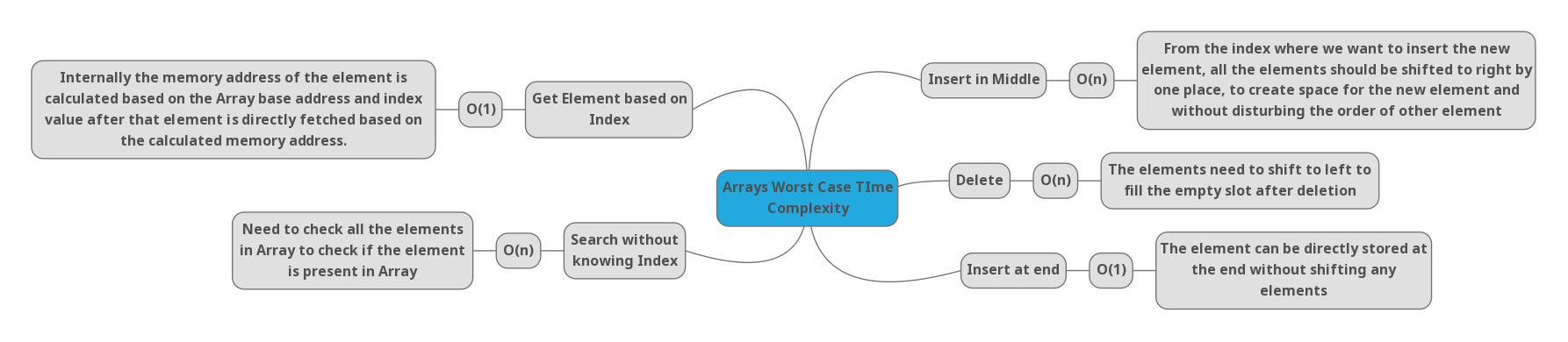
Arrays are one of the basic and important data structures to learn, They take constant time to read and Insert elements at the end and takes a linear time for the remaining.


Stack takes constant time for Push, Pop & Peek operations.

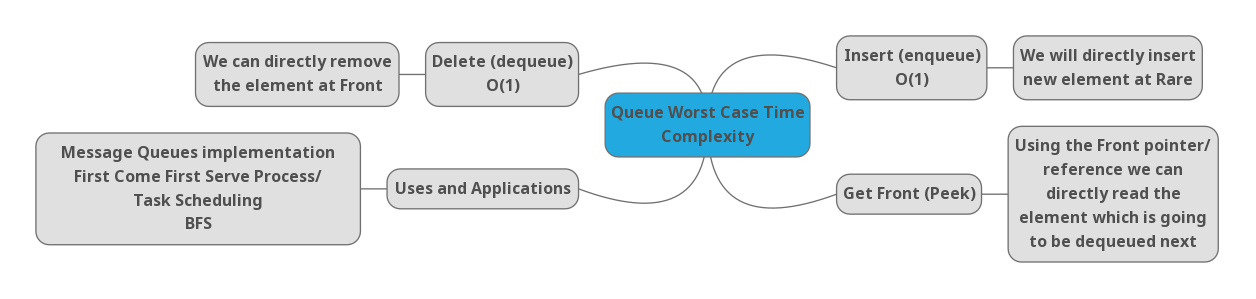
In Queue for Enqueue, Dequeue & Peek operations it takes only Constant time.

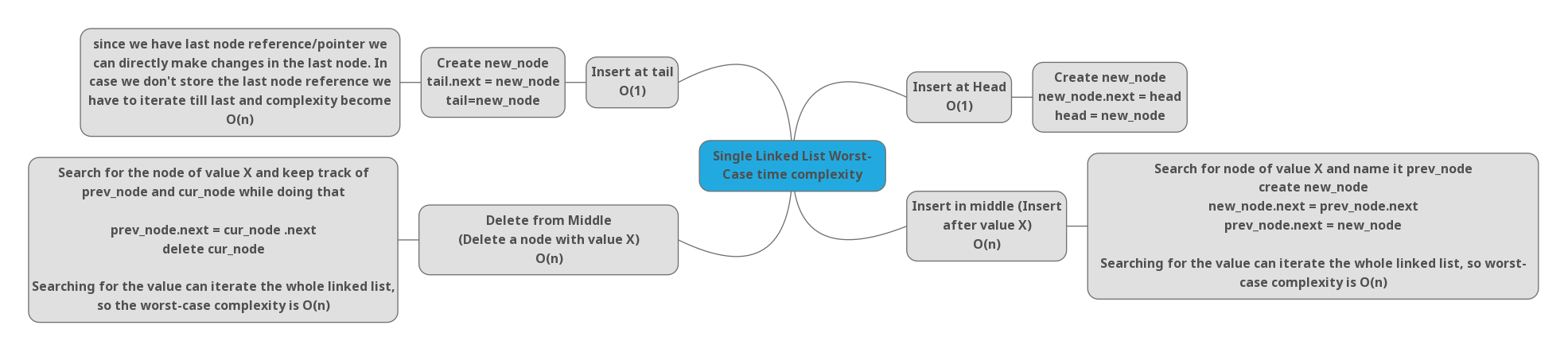
Here we are considering we are using tails for all single linked lists (Some implementations might not have it). Linked List is the data structure that comes with a lot of different operational scenarios, we have to think about head & tail usage in every operation we are doing. And operation logic and complexity changes at the head, tail, and middle. Typically insertion at head & tail takes constant time and insertion in middle takes linear time. Search can take linear time. Deletion at the head takes constant time and it can take linear time in remaining scenarios.
Trees: basic concepts
A tree is a data structure where a node can have zero or more children. Each node contains a value. Like graphs, the connection between nodes is called edges. A tree is a type of graph, but not all of them are trees (more on that later).
These data structures are called "trees" because the data structure resembles a tree 🌳. It starts with a root node and branch off with its descendants, and finally, there are leaves.

Here are some properties of trees:
- The top-most node is called root.
- A node without children is called leaf node or terminal node.
- Height (h) of the tree is the distance (edge count) between the farthest leaf to the root.
Ahas a height of 3Ihas a height of 0
- Depth or level of a node is the distance between the root and the node in question.
Hhas a depth of 2Bhas a depth of 1
- Implementing a simple tree data structure
As we saw earlier, a tree node is just a data structure that has a value and has links to their descendants.
Here's an example of a tree node:
1 | class TreeNode { |
We can create a tree with 3 descendents as follows:
1 |
|
That's all; we have a tree data structure!

The node abe is the root and bart, lisa and maggie are the leaf nodes of the tree. Notice that the tree's node can have a different number of descendants: 0, 1, 3, or any other value.
Tree data structures have many applications such as:
- Maps
- Sets
- Databases
- Priority Queues
- Querying an LDAP (Lightweight Directory Access Protocol)
- Representing the Document Object Model (DOM) for HTML on Websites.
Binary Trees
Trees nodes can have zero or more children. However, when a tree has at the most two children, then it's called binary tree.
Full, Complete and Perfect binary trees
Depending on how nodes are arranged in a binary tree, it can be full, complete and perfect:
- Full binary tree: each node has exactly 0 or 2 children (but never 1).
- Complete binary tree: when all levels except the last one are full with nodes.
- Perfect binary tree: when all the levels (including the last one) are full of nodes.
Look at these examples:

These properties are not always mutually exclusive. You can have more than one:
- A perfect tree is always complete and full.
- Perfect binary trees have precisely 2k-1 nodes, where
kis the last level of the tree (starting with 1).
- Perfect binary trees have precisely 2k-1 nodes, where
- A complete tree is not always
full.- Like in our "complete" example, since it has a parent with only one child. If we remove the rightmost gray node, then we would have a complete and full tree but not perfect.
- A full tree is not always complete and perfect.
Binary Search Tree (BST)
Binary Search Trees or BST for short are a particular application of binary trees. BST has at most two nodes (like all binary trees). However, the values are in such a way that the left children value must be less than the parent, and the right children is must be higher.
Duplicates: Some BST doesn't allow duplicates while others add the same values as a right child. Other implementations might keep a count on a case of the duplicity (we are going to do this one later).
Let's implement a Binary Search Tree!
BST Implementation
BST are very similar to our previous implementation of a tree. However, there are some differences:
- Nodes can have at most, only two children: left and right.
- Nodes values has to be ordered as
left < parent < right.
Here's the tree node. Very similar to what we did before, but we added some handy getters and setters for left and right children. Notice that is also keeping a reference to the parent and we update it every time add children.
TreeNode.jsCode
TreeNode.jsCode
1 | const LEFT = 0; |
Ok, so far we can add a left and right child. Now, let's do the BST class that enforces the left < parent < right rule.
BinarySearchTree.js linkUrl linkText
1 |
|
Let's implementing insertion.
BST Node Insertion
To insert a node in a binary tree, we do the following:
- If a tree is empty, the first node becomes the root and you are done.
- Compare root/parent's value if it's higher go right, if it's lower go left. If it's the same, then the value already exists so you can increase the duplicate count (multiplicity).
- Repeat #2 until we found an empty slot to insert the new node.
Let's do an illustration how to insert 30, 40, 10, 15, 12, 50:

We can implement insert as follows:
BinarySearchTree.prototype.addFull Code
1 | add(value) { |
We are using a helper function called findNodeAndParent. If we found that the node already exists in the tree, then we increase the multiplicity counter. Let's see how this function is implemented:
BinarySearchTree.prototype.findNodeAndParentFull Code
1 | findNodeAndParent(value) { |
findNodeAndParent goes through the tree searching for the value. It starts at the root (line 2) and then goes left or right based on the value (line 10). If the value already exists, it will return the node found and also the parent. In case that the node doesn't exist, we still return the parent.
BST Node Deletion
We know how to insert and search for value. Now, we are going to implement the delete operation. It's a little trickier than adding, so let's explain it with the following cases:
Deleting a leaf node (0 children)
1 | 30 30 |
We just remove the reference from node's parent (15) to be null.
Deleting a node with one child.
1 | 30 30 |
In this case, we go to the parent (30) and replace the child (10), with a child's child (15).
Deleting a node with two children
1 | 30 30 |
We are removing node 40, that has two children (35 and 50). We replace the parent's (30) child (40) with the child's right child (50). Then we keep the left child (35) in the same place it was before, so we have to make it the left child of 50.
Another way to do it to remove node 40, is to move the left child (35) up and then keep the right child (50) where it was.
1 | 30 |
Either way is ok as long as you keep the binary search tree property: left < parent < right.
Deleting the root.
1 | 30* 50 |
Deleting the root is very similar to removing nodes with 0, 1, or 2 children that we discussed earlier. The only difference is that afterward, we need to update the reference of the root of the tree.
Here's an animation of what we discussed.

In the animation, it moves up the left child/subtree and keeps the right child/subtree in place.
Now that we have a good idea how it should work, let's implement it:
BinarySearchTree.prototype.removeFull Code
1 | remove(value) { |
Here are some highlights of the implementation:
- First, we search if the node exists. If it doesn't, we return false and we are done!
- If the node to remove exists, then combine left and right children into one subtree.
- Replace node to delete with the combined subtree.
The function that combines left into right subtree is the following:
BinarySearchTree.prototype.combineLeftIntoRightSubtreeFull Code
1 | combineLeftIntoRightSubtree(node) { |
For instance, let's say that we want to combine the following tree and we are about to delete node 30. We want to mix 30's left subtree into the right one. The result is this:
1 | 30* 40 |
Now, and if we make the new subtree the root, then node 30 is no more!
Binary Tree Transversal
There are different ways of traversing a Binary Tree, depending on the order that the nodes are visited: in-order, pre-order, and post-order. Also, we can use them DFS and BFS that we learned from the graph post. Let's go through each one.
In-Order Traversal
In-order traversal visit nodes on this order: left, parent, right.
BinarySearchTree.prototype.inOrderTraversalFull Code
1 | inOrderTraversal(node = this.root) { |
Let's use this tree to make the example:
1 | 10 |
In-order traversal would print out the following values: 3, 4, 5, 10, 15, 30, 40. If the tree is a BST, then the nodes will be sorted in ascendent order as in our example.
Post-Order Traversal
Post-order traversal visit nodes on this order: left, right, parent.
BinarySearchTree.prototype.postOrderTraversalFull Code
1 | postOrderTraversal(node = this.root) { |
Post-order traversal would print out the following values: 3, 4, 5, 15, 40, 30, 10.
Pre-Order Traversal and DFS
In-order traversal visit nodes on this order: parent, left, right.
BinarySearchTree.prototype.preOrderTraversalFull Code
1 | preOrderTraversal(node = this.root) { |
Pre-order traversal would print out the following values: 10, 5, 4, 3, 30, 15, 40. This order of numbers is the same result that we would get if we run the Depth-First Search (DFS).
BinarySearchTree.prototype.dfsFull Code
1 | * dfs() { |
If you need a refresher on DFS, we covered in details on Graph post.
Breadth-First Search (BFS)
Similar to DFS, we can implement a BFS by switching the Stack by a Queue:
BinarySearchTree.prototype.bfsFull Code
1 | * bfs() { |
The BFS order is: 10, 5, 30, 4, 15, 40, 3
Balanced vs. Non-balanced Trees
So far, we have discussed how to add, remove and find elements. However, we haven't talked about runtimes. Let's think about the worst-case scenarios.
Let's say that we want to add numbers in ascending order.

We will end up with all the nodes on the left side! This unbalanced tree is no better than a LinkedList, so finding an element would take O(n). 😱
Looking for something in an unbalanced tree is like looking for a word in the dictionary page by page. When the tree is balanced, you can open the dictionary in the middle and from there you know if you have to go left or right depending on the alphabet and the word you are looking for.
We need to find a way to balance the tree!
If the tree was balanced, then we could find elements in O(log n) instead of going through each node. Let's talk about what balanced tree means.

If we are searching for 7 in the non-balanced tree, we have to go from 1 to 7. However, in the balanced tree, we visit: 4, 6, and 7. It gets even worse with larger trees. If you have one million nodes, searching for a non-existing element might require to visit all million while on a balanced tree it just requires 20 visits! That's a huge difference!
We are going to solve this issue in the next post using self-balanced trees (AVL trees).
Big O Notation
time complexity
it allow us to talk formally about how the runtime of an algorithm grows as the input grows.
n = number of operation the computer has to do can be: f(n) = n f(n) = n^2 f(n) = 1
f(n) = could be something entirely different !
O(n):
function addUpToSimple(n: number) {
let total = 0;
for (let i = 0; i < n; i++) {
total += i;
}
return total;
}
O(1):
function addUpComplex(n: number) {
return (n * (n + 1)) / 2;
}
O(n): maybe thinking O(2n) but we see big picture! BigONotation doesn't care about precision only about general trends linear? quadric? constant?
function printUpAndDown(n: number) {
console.log("Going up");
for (let i = 0; i < n; i++) {
console.log(i);
}
console.log("Going down");
for (let j = n - 1; j > 0; j--) {
console.log(j);
}
}
O(n^2)
function printAllPairs(n: number) {
for (let i = 0; i < n; i++) {
console.log(i);
for (let j = 0; j < n; j++) {
console.log(j);
}
}
}
O(n) : cuz as soon as n grows complexity grows too
function logAtLeastFive(n: number) {
for (let i = 0; i <= Math.max(5, n); i++) {
console.log(i);
}
}
O(1)
function logAtMostFive(n: number) {
for (let i = 0; i <= Math.min(5, n); i++) {
console.log(i);
}
}
space complexity
Rules of Thumb
- <==(most primitive booleans numbers undefined null are constant space)==>.
- <==(_**strings and reference types like objects an arrays require O(n) space _n is string length or number of keys**\)==>
O(1)
function sum(arr: number[]) {
let total = 0;
for (let i = 0; i < arr.length; i++) {
total += arr[i];
}
}
O(n)
function double(arr: number[]) {
const newArr = [];
for (let i = 0; i < arr.length; i++) {
array.push(arr[i] * 2);
}
return newArr;
}
quick note around object, array through BigO lens!
- object:
const person = { name: "John", age: 22, hobbies: ["reading", "sleeping"] };
Object.keys(person); // ["name", "age", "hobbies"] ---> O(n)
Object.values(person); // ["John", 22, Array(2)]---> O(n)
Object.entries(person); // [Array(2), Array(2), Array(2)]---> O(n)
person.hasOwnProperty("name"); // true ---> O(1)
- array:push() and pop() are always faster than unshift() and shift() because inserting or removing element from beginning of an array requires reIndexing all elements
Common Patterns
function binarySearch(sortedArr: number[], value: number): number {
let min = 0;
let max = sortedArr.length - 1;
while (min <= max) {
let middle = Math.floor((min + max) / 2);
if (sortedArr[middle] < value) {
min = middle + 1;
} else if (sortedArr[middle] > value) {
max = middle - 1;
} else {
return middle;
}
}
return -1;
}
Recursion
a process that calls itself
quick note around callStack
function wakeUp() {
// callStack [wakeUp]
takeShower();
eatBreakfast();
console.log("Ready to go ... ");
} // callStack []
function takeShower() {
// callStack [takeShower, wakeUp]
console.log("taking shower");
} // callStack[wakeUp]
function eatBreakfast() {
// callStack [eatBreakfast, wakeUp]
const meal = cookBreakFast();
console.log(`eating ${meal}`);
} // callStack [wakeUp]
function cookBreakFast() {
// callStack [cookBreakFast, eatBreakfast, wakeUp]
const meals = ["Cheese", "Protein Shake", "Coffee"];
return meals[Math.floor(Math.random() * meals.length)]; // callStack [eatBreakFast, wakeUp]
}
wakeUp();
two essential part of recursive functions
- base case : end of the line
- different input : recursive should call by different piece of data
function sumRange(num: number) {
if (num === 1) return 1;
return num + sumRange(num - 1);
}
function factorial(num: number) {
if (num === 1) return 1;
return num * factorial(num - 1);
}
helper method recursion vs pure recursion
// helper method recursion approach
function collectOdd(arr: number[]) {
const result = [];
function helper(helperArr: number[]) {
if (!helperArr.length) {
return;
}
if (helperArr[0] % 2 !== 0) {
result.push(helperArr[0]);
}
helper(helperArr.slice(1));
}
helper(arr);
return result;
}
// pure recursion approach
function collectOdd(arr: number[]): number[] {
let result = [];
if (!arr.length) {
return result;
}
if (arr[0] % 2 !== 0) {
result.push(arr[0]);
}
result = collectOdd(result.concat(arr.slice(1)));
return result;
}
Searching Algorithms
linear search
indexOf() includes() find() findIndex() all this methods doing linear search behind the scene
O(n)
function linearSearch(arr: number[], value: number): number {
for (let i = 0; i < arr.length; i++) {
if (arr[i] === value) {
return i;
}
return -1;
}
}
binary search
O(Log n)
function binarySearch(sortedArr: number[], value: number): number {
let left = 0;
let right = sortedArr.length - 1;
while (left <= right) {
const middle = Math.round((right + left) / 2);
if (sortedArr[middle] > value) {
right = middle - 1;
} else if (sortedArr[middle] < value) {
left = middle + 1;
} else {
return middle;
}
}
return -1;
}
Sorting Algorithms
array.sort()
array.sort(cb) will turn all values to string then sort it based on it's unicode
["a", "c", "b", "f", "d"].sort(); // (5) ["a", "b", "c", "d", "f"]
[1, 10, 6, 8, 2, 3, 5].sort(); //(7) [1, 10, 2, 3, 5, 6, 8]
/*
also receive callback function by two arguments:
a: previous number
b: next number
*/
// if callback return NEGATIVE number a will placed before b
[1, 10, 6, 8, 2, 3, 5].sort((a, b) => a - b); // (7) [1, 2, 3, 5, 6, 8, 10]
// if callback return POSITIVE number a will placed after b
(7)[(1, 2, 3, 5, 6, 8, 10)].sort((a, b) => b - a); // (7) [10, 8, 6, 5, 3, 2, 1]
// if callback return ZERO a and b will placed at the same position
Quadric
bubble sort
general: O(n^2) nearlySortedData: O(n)
function bubbleSort(arr: number[]): number[] {
for (let i = 0; i < arr.length; i++) {
let noSwap = true;
for (let j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
noSwap = false;
}
}
if (noSwap) break;
}
return arr;
}
// or
function bubbleSort(arr: number[]): number[] {
for (let i = arr.length; i > 0; i--) {
let noSwap = true;
for (let j = 0; j < i - 1; j++) {
if (arr[j] > arr[j + 1]) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
noSwap = false;
}
}
if (noSwap) break;
}
return arr;
}
selection sort
O(n^2)
function selectionSort(arr: number[]) {
for (let i = 0; i < arr.length; i++) {
let min = i;
for (let j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
if (min !== i) {
[arr[i], arr[min]] = [arr[min], arr[i]];
}
}
return arr;
}
insertion sort
general: O(n^2) nearlySortedData: O(n)
function insertionSort(arr) {
var currentVal;
for (let i = 1; i < arr.length; i++) {
currentVal = arr[i];
for (var j = i - 1; j >= 0 && arr[j] > currentVal; j--) {
arr[j + 1] = arr[j];
}
arr[j + 1] = currentVal;
}
return arr;
}
quadric sorting algorithms comparison
| Algorithm | Time Complexity (Best) | Time Complexity (Average) | Time Complexity (worst) | Space Complexity |
| bubble sort | O(n) | O(n^2) | O(n^2) | O(1) |
| insertion sort | O(n) | O(n^2) | O(n^2) | O(1) |
| selection sort | O(n^2) | O(n^2) | O(n^2) | O(1) |
Fancy
merge sort
O(n Log n)
// merge two sorted array
function merge(arr1: number[], arr2: number[]): number[] {
let result = [];
let i = 0;
let j = 0;
while (i < arr1.length && j < arr2.length) {
if (arr1[i] < arr2[j]) {
result.push(arr1[i]);
i++;
} else {
result.push(arr2[j]);
j++;
}
}
while (i < arr1.length) {
result.push(arr1[i]);
i++;
}
while (j < arr2.length) {
result.push(arr2[j]);
j++;
}
return result;
}
function mergeSort(arr: number[]): number[] {
if (arr.length <= 1) return arr;
const middle = Math.floor(arr.length / 2);
const left = mergeSort(arr.slice(0, middle));
const right = mergeSort(arr.slice(middle));
return merge(left, right);
}
quick sort

in following implementation we always assume first item as pivot
general: O(n Log n) sorted: O(n^2)
// place pivot in the right index and return pivot index
function pivot(arr: number[], start = 0, end = arr.length - 1) {
const pivot = arr[start];
let pivotIndex = start;
for (let i = start + 1; i < end; i++) {
if (arr[i] < pivot) {
pivotIndex++;
[arr[pivotIndex], arr[i]] = [arr[i], arr[pivotIndex]];
}
}
[arr[start], arr[pivotIndex]] = [arr[pivotIndex], arr[start]];
}
function quickSort(arr: number[], start = 0, end = arr.length - 1) {
if (left < right) {
const pivot = pivot(arr, start, end);
// left
quickSort(arr, start, pivotIndex - 1);
// right
quickSort(arr, pivotIndex + 1, end);
}
return arr;
}
radix sort
O(nk) n: the number of items we sorting k: average length of those numbers
// get the actual number at the given index
function getDigit(num: number, i: number): number {
return Math.floor(Math.abs(num) / Math.pow(10, i)) % 10;
}
// get number length
function digitCount(num: number): number {
if (num === 0) return 1;
return Math.floor(Math.log10(Math.abs(num))) + 1;
}
// return number by most length
function mostDigits(arr: number[]): number {
let maxDigits = 0;
for (let i = 0; i < arr.length; i++) {
maxDigits = Math.max(maxDigits, digitCount(arr[i]));
}
return maxDigits;
}
function radixSort(arr: number[]): number[] {
let maxDigitCount = mostDigits(arr);
for (let k = 0; k < maxDigitCount; k++) {
let digitBuckets = Array.from({ length: 10 }, () => []);
for (let j = 0; j < arr.length; j++) {
digitBuckets[getDigit(arr[j], k)].push(arr[j]);
}
arr = [].concat(...digitBuckets);
}
return arr;
}
fancy sorting algorithms comparison
| Algorithm | Time Complexity (Best) | Time Complexity (Average) | Time Complexity (worst) | Space Complexity |
| merge sort | O(n Log n) | O(n Log n) | O(n Log n) | O(n) |
| quick sort | O(n Log n) | O(n Log n) | O(n^2) | O(Log n) |
| radix sort | O(nk) | O(nk) | O(nk) | O(n + k) |
Data Structure
complexity comparison
| DataStructure | Insertion | Removal | Searching | Access |
| Singly Linked List | O(1) | bestCase(very beginning): O(1) worstCase(very end): O(n) | O(n) | O(n) |
| Doubly Linked List | O(1) | O(1) | O(n) it is faster than Singly Linked List | O(n) |
| Stack | O(1) | O(1) | O(n) | O(n) |
| Queue | O(1) | O(1) | O(n) | O(n) |
| Binary Search Tree | O( Log n) | - | O(Log n) | - |
| Binary Heap | O( Log n) | O( Log n) | O( n ) | - |
| Hash Tables | O( 1 ) | O( 1 ) | - | O( 1 ) |
Singly Linked list
class _Node {
constructor(public value: any) {}
public next: _Node | null = null;
}
class SinglyLinkedList {
private _length: number = 0;
private head: _Node | null = null;
private tail: _Node | null = null;
get length() {
return this._length;
}
get print(): null | _Node[] {
if (!this._length) return null;
const arr = [];
let currentNode = this.head;
while (currentNode) {
arr.push(currentNode.value);
currentNode = currentNode.next;
}
return arr;
}
public push(value: any): SinglyLinkedList {
const node = new _Node(value);
if (!this.head || !this.tail) {
this.head = node;
this.tail = this.head;
} else {
this.tail.next = node;
this.tail = node;
}
this._length += 1;
return this;
}
public pop(): _Node | null {
if (!this.head) return null;
let currentNode = this.head;
if (!currentNode.next) {
this.head = null;
this.tail = null;
this._length -= 1;
return currentNode;
}
while (currentNode.next && currentNode.next.next) {
currentNode = currentNode.next;
}
this.tail = currentNode;
this.tail.next = null;
this._length -= 1;
return currentNode.next as _Node;
}
public unShift(value: any): SinglyLinkedList {
const currentHead = this.head;
this.head = new _Node(value);
if (currentHead) {
this.head.next = currentHead;
} else {
this.tail = this.head;
}
this._length += 1;
return this;
}
public shift(): _Node | null {
if (!this.head) return null;
const currentHead = this.head;
this.head = currentHead.next;
this._length -= 1;
if (currentHead === this.tail) this.tail = null;
return currentHead;
}
public get(index: number): _Node | null {
if (index < 0 || index >= this._length) return null;
let currentNode = this.head;
for (let j = 0; j < index; j++) {
if (currentNode && currentNode.next) {
currentNode = currentNode.next;
}
}
return currentNode;
}
public set(index: number, value: any): _Node | null {
const node = this.get(index);
if (node) {
node.value = value;
}
return node;
}
public insert(index: number, value: any): SinglyLinkedList | null {
if (index < 0 || index >= this._length) {
return null;
} else if (index === 0) {
return this.unShift(value);
} else if (index === this._length) {
return this.push(value);
} else {
const prevNode = this.get(index - 1);
if (prevNode) {
const newNode = new _Node(value);
newNode.next = prevNode.next;
prevNode.next = newNode;
this._length += 1;
return this;
}
return prevNode;
}
}
public remove(index: number): _Node | null {
if (index === 0) {
return this.shift();
} else if (index === this._length - 1) {
return this.pop();
} else {
const prevNode = this.get(index - 1);
const currentNode = this.get(index);
if (prevNode && currentNode) {
prevNode.next = currentNode.next;
this._length -= 1;
}
return currentNode;
}
}
public reverse(): SinglyLinkedList | false {
if (this._length <= 1) return false;
let node = this.head;
this.head = this.tail;
this.tail = node;
let next: _Node | null;
let prev: _Node | null = null;
for (let i = 0; i < this._length; i++) {
if (node) {
next = node.next;
node.next = prev;
prev = node;
node = next;
}
}
return this;
}
}
Doubly Linked List
class _Node {
public next: _Node | null = null;
public prev: _Node | null = null;
constructor(public value: any) {}
}
class DoublyLinkedList {
private head: _Node | null = null;
private tail: _Node | null = null;
private _length = 0;
get length() {
return this._length;
}
get print(): null | _Node[] {
if (!this._length) return null;
const arr = [];
let currentNode = this.head;
while (currentNode) {
arr.push(currentNode.value);
currentNode = currentNode.next;
}
return arr;
}
public push(value: any): DoublyLinkedList {
const node = new _Node(value);
if (!this.tail) {
this.head = node;
} else {
this.tail.next = node;
node.prev = this.tail;
}
this._length += 1;
this.tail = node;
return this;
}
public pop(): _Node | null {
if (!this.tail) {
return null;
}
const currentTail = this.tail;
if (currentTail.prev) {
this.tail = currentTail.prev;
this.tail.next = null;
currentTail.prev = null;
} else {
this.head = null;
this.tail = null;
}
this._length -= 1;
return currentTail;
}
public shift(): null | _Node {
if (!this.head) {
return null;
}
const currentHead = this.head;
if (currentHead.next) {
this.head = currentHead.next;
this.head.prev = null;
currentHead.next = null;
} else {
return this.pop();
}
this._length -= 1;
return currentHead;
}
public unshift(value: any): DoublyLinkedList {
if (!this.head) {
return this.push(value);
}
const node = new _Node(value);
const currentHead = this.head;
this.head = node;
this.head.next = currentHead;
currentHead.prev = this.head;
this._length += 1;
return this;
}
public get(index: number): null | _Node {
if (index < 0 || index >= this._length) return null;
let currentNode: _Node | null = null;
if (index < Math.floor(this._length / 2)) {
// iterate from head to tail
currentNode = this.head;
for (let i = 0; i < index; i++) {
if (currentNode && currentNode.next) {
currentNode = currentNode.next;
}
}
} else {
// iterate from tail to head
currentNode = this.tail;
for (let i = this._length - 1; i > index; i--) {
if (currentNode && currentNode.prev) {
currentNode = currentNode.prev;
}
return currentNode;
}
}
return currentNode;
}
public set(index: number, value: any): _Node | null {
const node = this.get(index);
if (node) {
node.value = value;
}
return node;
}
public insert(index: number, value: any): DoublyLinkedList | null {
if (index < 0 || index > this._length) {
return null;
} else if (index === 0) {
return this.unshift(value);
} else if (index === this._length) {
return this.push(value);
} else {
const prevNode = this.get(index - 1);
const nextNode = this.get(index);
if (prevNode && nextNode) {
const newNode = new _Node(value);
prevNode.next = newNode;
(newNode.prev = prevNode), (newNode.next = nextNode);
nextNode.prev = newNode;
}
}
this._length += 1;
return this;
}
public remove(index: number): DoublyLinkedList | null {
if (index < 0 || index > this._length) {
return null;
} else if (index === 0) {
this.shift();
} else if (index === this._length - 1) {
this.pop();
} else {
const node = this.get(index);
if (node && node.prev && node.next) {
(node.prev.next = node.next), (node.next.prev = node.prev);
(node.next = null), (node.prev = null);
}
this._length -= 1;
}
return this;
}
}
Stacks
LIFO last in first out
// implement stack using array
const stack = [1, 2, 3];
stack.push(4); // [1,2,3,4]
stack.pop(); // [1,2,3]
// stacks just have push and pop
stack.unshift(0); // [0,1,2,3]
stack.shift(); // [1,2,3]
// implementing stack using singly linked list
class _Node {
public next: _Node | null = null;
constructor(public value: any) {}
}
class Stack {
private first: _Node | null = null;
private last: _Node | null = null;
private _length = 0;
get length(): number {
return this._length;
}
push(value: any): Stack {
const node = new _Node(value);
const currentFirst = this.first;
(this.first = node), (this.first.next = currentFirst);
if (!currentFirst) {
this.last = node;
}
this._length += 1;
return this;
}
pop(): _Node | null {
const currentFirst = this.first;
if (currentFirst) {
if (this.first === this.last) this.last = currentFirst.next;
this.first = currentFirst.next;
this._length -= 1;
}
return currentFirst;
}
}
Queue
FIFO first in first out
// implementing queue using array
const q = [];
q.push(1);
q.push(2);
q.shift(1); // out first items first
// or
q.shift(1);
q.shift(2);
q.pop(); // out first items first
// implementing queue using singly linked list
class _Node {
public next: _Node | null = null;
constructor(public value: any) {}
}
class Queue {
private first: _Node | null = null;
private last: _Node | null = null;
private _length = 0;
get length(): number {
return this._length;
}
enqueue(value: any): Queue {
const node = new _Node(value);
if (!this.last) {
(this.first = node), (this.last = node);
} else {
this.last.next = node;
this.last = node;
}
this._length += 1;
return this;
}
dequeue(): _Node | null {
const currentFirst = this.first;
if (currentFirst) {
if (this.first === this.last) this.last = null;
this.first = currentFirst.next;
this._length -= 1;
}
return currentFirst;
}
}
Tree
terminology
- root : top node of tree
- child : a node directly connected to another node when moving away from root
- parent : the converse notion of a child
- sibling : a group of nodes with the same parent
- leaf : a child with no children
- edge : connection from two node
binary search tree
- every parent node has at most two children
- every node to the left of parent node is always less than the parent
- every node to the right of parent node is always greater than the parent
class _Node {
constructor(public value: number) {}
public left: _Node | null = null;
public right: _Node | null = null;
}
class BinarySearchTree {
public root: _Node | null = null;
public insert(value: number): BinarySearchTree | null {
const node = new _Node(value);
if (!this.root) {
this.root = node;
} else {
let currentNode: _Node = this.root;
do {
if (value === currentNode.value) return null;
if (value < currentNode.value) {
if (currentNode.left) {
currentNode = currentNode.left;
} else {
currentNode.left = node;
break;
}
} else {
if (currentNode.right) {
currentNode = currentNode.right;
} else {
currentNode.right = node;
break;
}
}
} while (currentNode);
}
return this;
}
public have(value: number): boolean {
let currentNode = this.root;
while (currentNode) {
if (value === currentNode.value) {
return true;
} else {
if (value < currentNode.value) {
if (currentNode.left) {
currentNode = currentNode.left;
continue;
}
break;
} else {
if (currentNode.right) {
currentNode = currentNode.right;
continue;
}
break;
}
}
}
return false;
}
}
tree traversal
there is two main strategies to traversal a tree : Breadth-first-search and Depth-first-search
class _Node {
constructor(public value: number) {}
public left: _Node | null = null;
public right: _Node | null = null;
}
class BinarySearchTree {
public root: _Node | null = null;
public insert(value: number): BinarySearchTree | null {
const node = new _Node(value);
if (!this.root) {
this.root = node;
} else {
let currentNode: _Node = this.root;
do {
if (value === currentNode.value) return null;
if (value < currentNode.value) {
if (currentNode.left) {
currentNode = currentNode.left;
} else {
currentNode.left = node;
break;
}
} else {
if (currentNode.right) {
currentNode = currentNode.right;
} else {
currentNode.right = node;
break;
}
}
} while (currentNode);
}
return this;
}
public have(value: number): boolean {
let currentNode = this.root;
while (currentNode) {
if (value === currentNode.value) {
return true;
} else {
if (value < currentNode.value) {
if (currentNode.left) {
currentNode = currentNode.left;
}
break;
} else {
if (currentNode.right) {
currentNode = currentNode.right;
continue;
}
break;
}
}
}
return false;
}
/*
breadth first search (bfs) : traverse tree horizontally
*/
public bfs(): _Node[] {
const visited: _Node[] = [];
if (this.root) {
const q: _Node[] = [this.root];
while (q.length) {
if (q[0].left) q.push(q[0].left);
if (q[0].right) q.push(q[0].right);
visited.push(q[0]), q.shift();
}
}
return visited;
}
/*
depth first search (dfs) : traverse tree vertically
following contains three dfs searching methods:
1. preOrder : add node => going to left and add left => going to right and add right
2. postOrder : going to left and add left => going to right and add right => going to node and add node
3. inOrder : going to the left and add left => add node => going to the right and add right
*/
public dfsPreOrder(): _Node[] {
const visited: _Node[] = [];
if (this.root) {
(function traverse(node: _Node): void {
visited.push(node);
if (node.left) {
traverse(node.left);
}
if (node.right) {
traverse(node.right);
}
})(this.root);
}
return visited;
}
public dfsPostOrder(): _Node[] {
const visited: _Node[] = [];
if (this.root) {
(function traverse(node: _Node): void {
if (node.left) {
traverse(node.left);
}
if (node.right) {
traverse(node.right);
}
visited.push(node);
})(this.root);
}
return visited;
}
dfsInOrder(): _Node[] {
const visited: _Node[] = [];
if (this.root) {
(function traverse(node: _Node) {
if (node.left) {
traverse(node.left);
}
visited.push(node);
f;
if (node.right) {
traverse(node.right);
}
})(this.root);
}
return visited;
}
}
traversal comparison
depth-first vs breadth-first : they both timeComplexity is same but spaceComplexity is different if we got a wide tree like this:

breadth-first take up more space. cuz we adding more element to queue.
if we got a depth long tree like this:
depth-first take up more space.
potentially use cases for dfs variants (preOder postOrder inOrder) preOrder is useful when we want a clone of tree. inOrder is useful when we want data in order that it's stored in tree.
Binary heaps
terminology
- a binary heap is as compact as possible (all the children of each node are as full as they can be and left children and filled out first)
- each parent has at most two children
Max Binary Heap:
- parent nodes are always greater than child nodes but there is no guarantees between sibling
Min Binary Heap:
- child nodes are always greater than parent nodes but there is no guarantees between sibling
binary heap parent and child relations
class MaxBinaryHeap {
private _values: number[] = [];
get values(): number[] {
return this._values;
}
private sinkingUp(value: number): void {
let valueIndex = this._values.length - 1;
while (valueIndex > 0) {
const parentIndex = Math.floor((valueIndex - 1) / 2);
const parent = this._values[parentIndex];
if (value <= parent) break;
this._values[parentIndex] = value;
this._values[valueIndex] = parent;
valueIndex = parentIndex;
}
}
private sinkingDown(): void {
let targetIndex = 0;
while (true) {
let leftChildIndex = targetIndex * 2 + 1,
rightChildIndex = targetIndex * 2 + 2;
let target = this._values[targetIndex],
leftChild = this._values[leftChildIndex],
rightChild = this._values[rightChildIndex];
if (target < leftChild && target < rightChild) {
if (rightChild > leftChild) {
[
this._values[targetIndex],
this._values[rightChildIndex]
] = [
this._values[rightChildIndex],
this._values[targetIndex]
];
targetIndex = rightChildIndex;
} else {
[
this._values[targetIndex],
this._values[leftChildIndex]
] = [
this._values[leftChildIndex],
this._values[targetIndex]
];
targetIndex = leftChildIndex;
}
continue;
} else if (rightChild >= target) {
[this._values[targetIndex], this._values[rightChildIndex]] = [
this._values[rightChildIndex],
this._values[targetIndex]
];
targetIndex = leftChildIndex;
continue;
} else if (leftChild >= target) {
[this._values[targetIndex], this._values[leftChildIndex]] = [
this._values[leftChildIndex],
this._values[targetIndex]
];
targetIndex = leftChildIndex;
continue;
}
break;
}
}
public insert(value: number): number[] {
this._values.push(value);
this.sinkingUp(value);
return this._values;
}
public extractMax(): number | null {
if (!this._values.length) {
return null;
}
const root = this._values[0];
this._values[0] = this._values[this._values.length - 1];
this._values.pop();
this.sinkingDown();
return root;
}
}
Priority Queue
A data structure which every element has a priority. Elements with higher priorities are served before elements with lower priorities.
In the following example, we implemented a priority queue using minBinaryHeap but you should know binaryHeaps and priority queue is two different concepts and we just use an abstract of it
interface INode {
value: any;
priority: number;
}
class _Node implements INode {
constructor(public value: any, public priority: number = 0) {}
}
class PriorityQueue {
private _values: INode[] = [];
get values(): INode[] {
return this._values;
}
private sinkingUp(node: INode): void {
let valueIndex = this._values.length - 1;
while (valueIndex > 0) {
const parentIndex = Math.floor((valueIndex - 1) / 2);
const parent = this._values[parentIndex];
if (node.priority >= parent.priority) break;
this._values[parentIndex] = node;
this._values[valueIndex] = parent;
valueIndex = parentIndex;
}
}
private sinkingDown(): void {
let targetIndex = 0;
while (true) {
let leftChildIndex = targetIndex * 2 + 1,
rightChildIndex = targetIndex * 2 + 2;
let target = this._values[targetIndex],
leftChild = this._values[leftChildIndex],
rightChild = this._values[rightChildIndex];
if (
leftChild &&
rightChild &&
target.priority > leftChild.priority &&
target.priority > rightChild.priority
) {
if (rightChild.priority < leftChild.priority) {
[
this._values[targetIndex],
this._values[rightChildIndex]
] = [
this._values[rightChildIndex],
this._values[targetIndex]
];
targetIndex = rightChildIndex;
} else {
[
this._values[targetIndex],
this._values[leftChildIndex]
] = [
this._values[leftChildIndex],
this._values[targetIndex]
];
targetIndex = leftChildIndex;
}
continue;
} else if (rightChild && rightChild.priority <= target.priority) {
[this._values[targetIndex], this._values[rightChildIndex]] = [
this._values[rightChildIndex],
this._values[targetIndex]
];
targetIndex = leftChildIndex;
continue;
} else if (leftChild && leftChild.priority <= target.priority) {
[this._values[targetIndex], this._values[leftChildIndex]] = [
this._values[leftChildIndex],
this._values[targetIndex]
];
targetIndex = leftChildIndex;
continue;
}
break;
}
}
public enqueue({ value, priority }: INode): _Node[] {
const node = new _Node(value, priority);
this._values.push(node);
this.sinkingUp(node);
return this._values;
}
public dequeue(): _Node | null {
if (!this._values.length) {
return null;
}
const root = this._values[0];
this._values[0] = this._values[this._values.length - 1];
this._values.pop();
this.sinkingDown();
return root;
}
}
Hash Tables
Hash tables are collection of key-value pairs
collisions
There is possibility for handle collisions is hash tables :
- Separate chaining ( e.g. using nested arrays of key values implemented in following hash tables )
- linear probing ( if index filled place {key, value} in next position )
type El = [string, any];
class HashTable {
private keyMap: El[][];
constructor(size: number = 53) {
this.keyMap = new Array(size);
}
public _hash(key: string): number {
let total = 0;
const WEIRD_PRIME = 31;
for (let i = 0; i < key.length; i++) {
const characterCode = key.charCodeAt(i) - 96;
total = (total + characterCode * WEIRD_PRIME) % this.keyMap.length;
}
return total;
}
set(key: string, value: any): El[][] {
const index = this._hash(key);
if (!this.keyMap[index]) {
this.keyMap[index] = [];
}
this.keyMap[index].push([key, value]);
return this.keyMap;
}
get(key: string): El | undefined {
const index = this._hash(key);
const elements = this.keyMap[index];
if (elements) {
for (let value of elements) {
if (value[0] === key) return value[1];
}
}
return undefined;
}
get keys(): string[] {
const keys: string[] = [];
for (let value of this.keyMap) {
if (value) {
for (let _value of value) {
keys.push(_value[0]);
}
}
}
return keys;
}
get values(): any[] {
const values = new Set<any>();
for (let value of this.keyMap) {
if (value) {
for (let _value of value) {
values.add(value[1]);
}
}
}
return [...values];
}
}
Graphs
A graph data structure consists of a finite (and possibly mutable) set of vertices or nodes or points, together with a set of unordered pairs of these vertices for an undirected graph or a set of ordered pairs for directed graph.
terminology
- vertex :node
- edge : connection between nodes
- directed/ undirected graph: in directed graph there is a direction assigned to vertices an in undirected no direction assigned.
- weighted/ unweighted graph:
in weighted graph there is a weight associated by edges but in unweighted graph no weight assigned to edges

adjacency matrix

adjacency list

adjacency list vs adjacency matrix
| Operation | Adjacency List | Adjacency Matrix |
| Add vertex | O(1) | O(V^2) |
| Add Edge | O(1) | O(1) |
| Remove vertex | O(V+E) | O(V^2) |
| Remove Edge | O(E) | O(1) |
| Query | O(V+E) | O(1) |
| Storage | O(V+E) | O(V^2) |
- |V| : number of Vertices
- |E| : number of Edges
- Adjacency List take less space in sparse graph( when we have a few edges ).
- Adjacency List are faster to iterate over edges.
- Adjacency Matrix are faster to finding a specific edge.
graph(adjacency list)
interface AdjacencyList {
[vertex: string]: string[];
}
class Graph {
private _adjacencyList: AdjacencyList = {};
public get adjacencyList(): AdjacencyList {
return this._adjacencyList;
}
public set adjacencyList(value: AdjacencyList) {
this._adjacencyList = value;
}
public addVertex(vertex: string): AdjacencyList {
this._adjacencyList[vertex] = [];
return this._adjacencyList;
}
public addEdge(vertex1: string, vertex2: string): boolean {
if (this._adjacencyList[vertex1] && this._adjacencyList[vertex2]) {
this._adjacencyList[vertex1].push(vertex2),
this._adjacencyList[vertex2].push(vertex1);
return true;
}
return false;
}
public removeEdge(vertex1: string, vertex2: string): boolean {
if (this._adjacencyList[vertex1] && this._adjacencyList[vertex2]) {
(this._adjacencyList[vertex1] = this._adjacencyList[vertex1].filter(
(value: string) => value !== vertex2
)),
(this._adjacencyList[vertex2] = this._adjacencyList[
vertex2
].filter((value: string) => value !== vertex1));
return true;
}
return false;
}
public removeVertex(vertex: string): string | undefined {
if (this._adjacencyList[vertex]) {
for (let key in this._adjacencyList) {
this.removeEdge(key, vertex);
}
delete this._adjacencyList[vertex];
return vertex;
}
return undefined;
}
}
Graph Traversal
depth first traversal and breadth first traversal in graph
interface AdjacencyList {
[vertex: string]: string[];
}
class Graph {
private _adjacencyList: AdjacencyList = {};
public get adjacencyList(): AdjacencyList {
return this._adjacencyList;
}
public set adjacencyList(value: AdjacencyList) {
this._adjacencyList = value;
}
public addVertex(vertex: string): AdjacencyList {
this._adjacencyList[vertex] = [];
return this._adjacencyList;
}
public addEdge(vertex1: string, vertex2: string): boolean {
if (this._adjacencyList[vertex1] && this._adjacencyList[vertex2]) {
this._adjacencyList[vertex1].push(vertex2),
this._adjacencyList[vertex2].push(vertex1);
return true;
}
return false;
}
public removeEdge(vertex1: string, vertex2: string): boolean {
if (this._adjacencyList[vertex1] && this._adjacencyList[vertex2]) {
(this._adjacencyList[vertex1] = this._adjacencyList[vertex1].filter(
(value: string) => value !== vertex2
)),
(this._adjacencyList[vertex2] = this._adjacencyList[
vertex2
].filter((value: string) => value !== vertex1));
return true;
}
return false;
}
public removeVertex(vertex: string): string | undefined {
if (this._adjacencyList[vertex]) {
for (let key in this._adjacencyList) {
this.removeEdge(key, vertex);
}
delete this._adjacencyList[vertex];
return vertex;
}
return undefined;
}
public dfcRecursive(startingVertex: string): string[] {
const results: string[] = [];
const adjacencyList = this._adjacencyList;
let currentVertex = this._adjacencyList[startingVertex];
if (currentVertex) {
const visitedVertex: { [vertex: string]: boolean } = {};
(function traverse(vertex: string | undefined): void {
if (!vertex) return;
if (!visitedVertex[vertex]) {
visitedVertex[vertex] = true;
results.push(vertex);
for (let neighbor of currentVertex) {
if (!visitedVertex[neighbor]) {
currentVertex = adjacencyList[neighbor];
traverse(neighbor);
}
}
}
})(startingVertex);
}
return results;
}
// or
public dfsIterative(startingVertex: string): string[] {
const results: string[] = [];
if (this._adjacencyList[startingVertex]) {
let stack: string[] = [startingVertex];
const visitedVertex: { [vertex: string]: boolean } = {};
while (stack.length) {
debugger;
const currentVertex = stack.pop();
if (currentVertex && !visitedVertex[currentVertex]) {
visitedVertex[currentVertex] = true;
results.push(currentVertex);
stack = [...stack, ...this._adjacencyList[currentVertex]];
}
}
}
return results;
}
public breadthFirstSearch(startingVertex: string): string[] {
const results: string[] = [];
if (this._adjacencyList[startingVertex]) {
let queue = [startingVertex];
const visitedVertex: { [vertex: string]: boolean } = {};
while (queue.length) {
const currentVertex = queue.shift();
if (currentVertex && !visitedVertex[currentVertex]) {
visitedVertex[currentVertex] = true;
results.push(currentVertex);
queue = [...queue, ...this._adjacencyList[currentVertex]];
}
}
}
return results;
}
}
Dijkstra's Shortest path firt Algorithms
Finding shortest path between two vertices in a weighted graph.

interface Value {
value: any;
priority: number;
}
interface Neighbor {
vertex: string;
weight: number;
}
interface AdjacencyList {
[vertex: string]: Neighbor[];
}
// naive priority queue
class PriorityQueue {
private _values: Value[] = [];
public get values(): Value[] {
return this._values;
}
public enqueue(value: any, priority: number): Value[] {
this._values.push({ value, priority });
this.sort();
return this._values;
}
public dequeue(): Value {
const value = this._values.shift();
return value as Value;
}
private sort() {
this._values.sort((a: Value, b: Value) => a.priority - b.priority);
}
}
class WeightedGraph {
private _adjacencyList: AdjacencyList = {};
public get adjacencyList(): AdjacencyList {
return this._adjacencyList;
}
public set adjacencyList(value: AdjacencyList) {
this._adjacencyList = value;
}
public addVertex(vertex: string): AdjacencyList {
this._adjacencyList[vertex] = [];
return this._adjacencyList;
}
public addEdge(vertex1: string, vertex2: string, weight: number): boolean {
if (this._adjacencyList[vertex1]) {
this._adjacencyList[vertex1].push({ vertex: vertex2, weight });
this._adjacencyList[vertex2].push({ vertex: vertex1, weight });
return true;
}
return false;
}
/*
dijkstra shortest path first
*/
dijkstraSPF(startingVertex: string, targetVertex: string): string[] {
let path: string[] = [];
if (
this._adjacencyList[startingVertex] &&
this._adjacencyList[targetVertex]
) {
const pq = new PriorityQueue();
const previousVertex: { [vertex: string]: string | null } = {};
const distances: { [vertex: string]: number } = {};
// build initial states
for (let key in this._adjacencyList) {
if (key === startingVertex) {
(distances[key] = 0), pq.enqueue(key, 0);
} else {
distances[key] = Infinity;
pq.enqueue(key, Infinity);
}
previousVertex[key] = null;
}
while (pq.values.length) {
let smallest = pq.dequeue().value;
if (smallest) {
if (smallest === targetVertex) {
// done build path
while (
previousVertex[smallest] ||
smallest === startingVertex
) {
path.push(smallest);
smallest = previousVertex[smallest];
}
break;
}
for (let neighbor of this._adjacencyList[smallest]) {
const candidate = distances[smallest] + neighbor.weight;
let nextNeighbor = neighbor.vertex;
if (candidate < distances[nextNeighbor]) {
distances[nextNeighbor] = candidate;
previousVertex[nextNeighbor] = smallest;
pq.enqueue(nextNeighbor, candidate);
}
}
}
}
}
return path.reverse();
}
}
Dynamic Programming (light introduction)
It's a method for solving a complex problems by breaking it down into a collection of simpler problems, solving their subProblems once and storing their solutions. technically it using knowledge of last problems to solve next by memorization
example Fibonacci sequence
Let's implement it without dynamic programming:without dynamic programming:
in fibonacci sequence fib(n) = fib(n-2) + fib(n-1) && fin(1) = 1 && fib(2) = 1
O(2^n)
function fib(n: number): number {
if (n <= 2) return 1;
return fib(n - 1) + fib(n - 2);
}

As you see we calculate f(5) two times with current implementation.
memorization
Storing the results of expensive function class and returning the cached result when the same inputs occur again.
O(n)
function fib(n: number, memo: number[] = []): number {
if (memo[n]) return memo[n];
if (n <= 2) return 1;
const res = fib(n - 1, memo) + fib(n - 2, memo);
memo[n] = res;
return res;
}
fib(10000); // Maximum callStack exceeded
tabulation
function fib(n: number): number {
if (n <= 2) return 1;
const fibNumbers = [0, 1, 1];
for (let index = 3; index <= n; index++) {
fibNumbers[index] = fibNumbers[index - 1] + fibNumbers[index - 2];
}
console.log(fibNumbers);
return fibNumbers[n];
}
fib(10000); // Infinity
Interesting Stuff
// turn it to boolean
console.log(!!1); // true
console.log(!!0); // false
// group operation
(newNode.prev = prevNode), (newNode.next = nextNode);
String
const str = "hello";
str.search('lo') || .indexOf('lo') // 3
str.includes('lo') // true
string pattern matching
// regex.test(str: number) Returns a Boolean value that indicates whether or not a pattern exists in a searched string.
function charCount(str: string) {
const result: { [key: string]: number } = {};
for (let char of str) {
char = char.toLowerCase();
if (/[a-z0-9]/.test(char)) {
result[char] = ++result[char] || 1;
}
}
return result;
}
// *** string.chatCodeAt(i: number) Returns the unicode of value on specified location
/*
numeric (0-9) code > 47 && code < 58;
upper alpha (A-Z) code > 64 && code < 91;
lower alpha (a-z) code > 96 && code <123;
*/
function charCount(str: string) {
const result: { [key: string]: number } = {};
for (let char of str) {
if (isAlphaNumeric(char)) {
char = char.toLowerCase();
result[char] = ++result[char] || 1;
}
}
return result;
}
function isAlphaNumeric(char: string) {
const code = char.charCodeAt(0);
if (
!(code > 47 && code < 58) &&
!(code > 64 && code < 91) &&
!(code > 96 && code < 123)
) {
return false;
}
return true;
}
Array
const array = ["hello", "world"];
arr.find((el) => el === "world"); // world
arr.findIndex((el) => el === "world"); // 1
[1, 2].includes(1); // true
Array.from({ length: 2 }, () => ["lol"]); // [["lol"], ["lol"]]
const stack = ["A", "B", "D", "E", "C", "F"];
const s = stack.shift();
const p = stack.pop();
console.log(s); // "A"
console.log(p); // "F"
["a", "b"].reverse(); // ['b', 'a']
Object
delete this._adjacencyList[vertex]; // delete key and value from object
delete this._adjacencyList.vertex;
Map
const map = new Map();
// store any type of **unique key** of use duplicate key it will override last value
map.set({ 1: "Object" }, "Object");
map.set(["arr"], "arr");
map.set(1, "number");
map.set(false, "boolean");
map.set(() => console.log("Function"), "Function");
console.log(map);
/*
0: {Object => "Object"}
1: {Array(1) => "arr"}
2: {1 => "number"}
3: {false => "boolean"}
4: {function () { return console.log("Function"); } => "Function"}
*/
// iterable by **for (let [key, value] of map)**
for (let [key, value] of map) console.log(key, value);
// map to arr
const arr = [...map]; // :[ [key, value] ]
/*
0: (2) [{…}, "Object"]
1: (2) [Array(1), "arr"]
2: (2) [1, "number"]
3: (2) [false, "boolean"]
4: (2) [ƒ, "Function"]
*/
Math
Math.pow(2, 2); // 4
Math.abs(-5); // 5
Math.log10(100); // 10
Math.max(...[1, 2, 3]); // 3
Math.min(...[1, 2, 3]); // 1
